For the scheduled spot time differences that have a non-zero ratio of conflicts, we can store and plot the combination of push back times that lead to conflicts. In Figure B the vertical axis represents the push back time of aircraft $A(i)$, $PB^A$, and the horizontal axis represents the push back time of aircraft $BR(j)$, $PB^{BR}$. In the Figure we color select cross sections to demonstrate the relationship between the ratio of conflicts (left panel) defined by the difference between their scheduled spot times and the set of red conflict points (right panel) defined by the combination of push back times that lead to conflicts for the given difference between their scheduled spot times $t_j - t_i$.

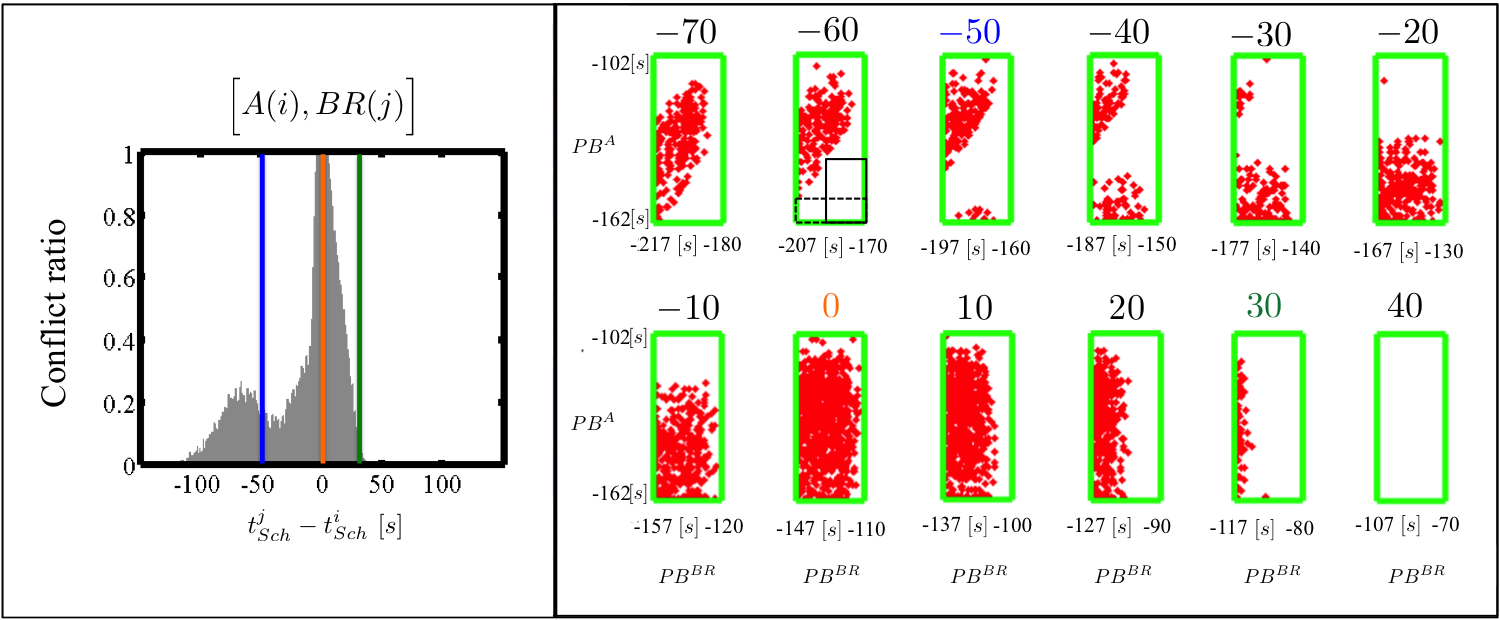
The combinations of push back times that lead to conflicts between aircraft $A(i)$ and $BR(j)$ are plotted in 10s increments for the spot time differences ranging from $t_j - t_i = -70$ to $t_j - t_i = 40$. Given that we are interested in the scheduled spot time difference between two aircraft, we fix the spot time of aircraft $A(i)$ such that $t_A = 0$, and the difference in the scheduled spot time is defined by the spot time of aircraft $BR(j)$. Associated with each difference in scheduled spot time, i.e., $t_{BR} = -70$, is a green rectangle that is defined by the earliest and latest feasible push back times for each aircraft such that the spot time of the schedule is satisfied. Thus, in order to satisfy the spot time $t_A = 0$, aircraft $A(i)$ must push back within the window $PB^A \in [-162,-102]$ and to satisfy the spot time $t_{BR} = -70$ aircraft $BR(j)$ must push back within $PB^{BR} \in [-217,-180]$. For $-70$ there is a set of combination of push back times that lead to conflicts. These combinations are labeled as red points within the green rectangle.

Consider the distribution of red conflict points for the scheduled spot time difference of $-60$ seen in the right panel of the Figure. We observe that in the bottom right of the green rectangle there is a large area that does not contain any red conflict points. If we restrict aircraft $A(i)$ and $B(j)$ to push back within the lower right corner of the green rectangle then we can ensure conflict free trajectories. Two potential solutions are shown where the first solution is shown with a solid black line and the second solution with a dotted black line. Among all possible solutions we would like to find a combination of push back time windows where the minimum time window is maximized.

The objective function is defined as \begin{align} \max_{t_i^S,t_i^F,t_j^S,t_j^F}& \,\,\,\,\, \,\,\,\,\, J: = \left[ M + \epsilon (t_i^F-t_i^S+t_j^F-t_j^S) \right] \label{objective} \end{align} where $M = \min \{ t_i^F -t_i^S, t_j^S - t_j^F \} $ is the minimum time window among both aircraft $i$ and $j$ and $\epsilon$ is sufficiently small. In the objective function the extra term multiplied by $\epsilon$ is added in order to distinguish between two combinations of time windows that have equal minimum edge lengths.

For departing aircraft $i,j \in D$ we introduce the two constraints \begin{align} t_i^F - t_i^S - M &\geq 0 \label{m_const} \\ t_j^F - t_j^S - M &\geq 0 \end{align} that ensure the push back time window for aircraft $i$ and the push back time window for aircraft $j$ are both greater than the minimum time window $M$. We note that the value $M$ is not a fixed value, but a function of the four variables we solve for.

Similarly, for departing aircraft $i,j \in D$ we introduce the two constraints \begin{align} t_i^F - t_i^S - \delta_{min} &\geq 0 \label{del1} \\ t_j^F - t_j^S - \delta_{min} &\geq 0 \label{del2} \end{align} that ensure the push back time windows for aircraft $i$ and $j$ are both larger than a predefined value $\delta_{min}$. The value $\delta_{min}$ is the minimum acceptable push back window. For example, pilots and ramp area ground crew could find a schedule that requires aircraft to initiate push back within a window of 5 seconds too restrictive to consistently execute. In this paper we use the value $\delta_{min} =25 [s]$ when solving for the optimal sub-windows. The correct value should be determined in conjunction by ramp area controllers and pilots.

For departing aircraft $i,j \in D$ we introduce the four constraints \begin{align} t_i^S - t_i - t_i^{S0} &\geq 0 \label{eqn_green} \\ t_i^F - t_i - t_i^{F0} &\leq 0 \\ t_j^S - t_j - t_j^{S0} &\geq 0 \\ t_j^F - t_j - t_j^{F0} &\leq 0 \label{eqn_green2} \end{align} where $t_i $ is the taxiway spot time of aircraft $i$ and $t_i^{S0}$ and $t_i^{F0}$ are the earliest and latest feasible push back times for aircraft $i$ such that the scheduled spot time $t_i=0$ is enforced. The same definitions apply to the variables for aircraft $j$. For the scheduled spot time $t_i=0$, the earliest feasible push back time is defined by $t_i^{S0} = - \text{max}_i \,\, (T_i)$ and the latest feasible push back time is defined by $t_i^{F0} = - \text{min}_i \,\, (T_i)$ . The variable $T_i$ is the trajectory duration of aircraft $i$ that is sampled from the stochastic model. For any given relative schedule, the earliest and latest feasible push back times define the green edges of the rectangle that are seen in the Figure. The distribution in trajectory duration is estimated from the robot experiment data which is directly influenced by the human operator.

The previous four constraints ensure that for any given combination of spot time schedules, given by $t_i$ and $t_j$, the start and end of the push back sub-windows defined by $t^S$ and $t^F$ must be within the bounds defined by the earliest and latest feasible push back times. This implies satisfying these constraints ensures that there exists a feasible trajectory for aircraft $i/j$ that is capable of meeting the scheduled spot times $t_i/t_j$ without accounting for conflicts. These four constraints provide that the push back windows that we solve for, which are illustrated in black solid (dotted) lines in Fig.~\ref{formulation}, are indeed sub-windows of the original green rectangle.

For each conflict point $\kappa = (PB^{BR} , PB^A)$, we introduce the five constraints. \begin{align} z_{\kappa 1} \Big[ t_i^F - PB^A \Big] & \leq 0 \label{new1} \\ z_{\kappa 2} \Big[ t_i^S - PB^A \Big] &\geq 0 \\ z_{\kappa 3} \Big[ t_j^F - PB^{BR} \Big] & \leq 0 \\ z_{\kappa 4} \Big[ t_j^S - PB^{BR} \Big] &\geq 0 \label{new4} \\ z_{\kappa 1} + z_{\kappa 2} + z_{\kappa 3} + z_{\kappa 4} &= 1 \label{new5} \end{align} where this set of constraints enforces that the conflict point $\kappa$ is not a convex combination of the start and end times of the optimal combination of sub-windows defined by $(t_i^S,t_i^F,t_j^S,t_j^F)$. Geometrically speaking, this set of five constraints ensures that any feasible combination of sub-window is either above, below, left or right of the conflict point $\kappa$. These constraints can be linearized as

where the value of S is sufficiently large.