The conflict distributions can be applied to optimize departing and arriving traffic within the Charlotte Douglass (CLT) center alley. The proposed approach is conservative in nature because the separation constraints we define will ensure a zero ratio of conflict. Given a set of departing aircraft $i \in D$ available to push back from their gates at time $\alpha_i$ and a set of arriving aircraft $i \in A$ that are available to be released from node P2 into the ramp area at time $\beta_i$, we consider finding a sequence of merge node times $t_i$ that ensure conflict free trajectories. The optimal sequence of merge node times is defined as the schedule that minimizes the sum of aircraft hold time for both departing and arriving aircraft. The objective function is given by \begin{align} &\min \left[ \sum_{i \in D} \Big(t_i - (\alpha_i + | t_i^{S0} | ) \Big) + \,\,\sum_{i \in A} (t_i - \beta_i) \right] \label{objective} \end{align} where $t_i^{S0}$ is the earliest feasible push back time for departing aircraft $i$ such that the scheduled time $t_i =0$ is enforced. The value $|t_i^{S0}|$ is equal to the longest duration feasible trajectory that is sampled from the stochastic model. For departing aircraft $i$, the difference between the scheduled terminal time $t_i$ and the earliest available push back time plus duration of the longest feasible trajectory, $(\alpha_i + | t_i^{S0} | )$, describes the hold time for the individual aircraft. Departing aircraft are only held at the gate. After being cleared to push back, departing aircraft are not held and are assumed to begin the taxi when they finish spooling the engines.

For arriving aircraft $i$, the difference between the scheduled time $t_i$ and the earliest available release time $\beta_i$ describes the hold time for the individual aircraft. Arrival aircraft are assumed to be held at merge node P2 prior to being released into the ramp area. Thus, within the objective function the total aircraft hold time for departing and arriving aircraft are given by the summations.

For all departing aircraft $i \in D$ we introduce the constraint \begin{align} t_i - (\alpha_i + | t_i^{S0} | ) \geq& 0 \,\,\,\,\,\, \,\,\, \,\,\,\,\,\, \,\,\,\,\,\,\,\,\, \,\,\, \forall i \in D \end{align} where this constraint ensures that for departing aircraft $i$ the scheduled time of arrival $t_i$ at merge node P1 is greater than the earliest available push back time $\alpha_i$ plus the duration of the longest feasible trajectory $|t_i^{S0}|$.

Similarly for all arriving aircraft $i \in A$ we have the constraint \begin{align} t_i - \beta_i \geq& 0 \,\,\,\,\,\, \,\,\, \,\,\,\,\,\, \,\,\,\,\,\,\,\,\, \,\,\, \forall i \in A \end{align} which ensures that for arriving aircraft $i$ the scheduled time $t_i$ that we release the aircraft from merge node P2 into the ramp area is greater than the earliest time $\beta_i$ that the aircraft is available to be released. Constraints (8) and (9) in conjunction ensure that the hold time of any individual departing or arriving aircraft within the objective function is strictly non-negative, i.e., the minimum hold time for any aircraft $i$ is equal to zero.

For all departing aircraft $i,j \in D$ we introduce a sequencing constraint defined at merge node P1 given by

where $z_{ij}$ is a binary variable that is $1$ if departing aircraft $j$ follows departing aircraft $i$ at merge node P1, else $z_{ij} =0$. For all departing aircraft $i,j \in D$ we have the separation constraint

which ensures that if departing aircraft $j$ follows departing aircraft $i$ at merge node P1 they should be separated by a minimum of $\delta_{ij}$, else the constraint is automatically satisfied. Given the sequencing constraint defined in (10), the value $\delta_{ij}$ should be non-negative else the constraint can not be satisfied.

Similarly for all arriving aircraft $i,j \in A$ we introduce the sequencing constraint \begin{align} Z_{ij}^{*} + Z_{ji}^{*} =& 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \forall i,j \in A \end{align} where $Z_{ij}^*$ is a binary variable that is $1$ if arriving aircraft $j$ follows arriving aircraft $i$ at merge node P2, else $Z_{ij}^* =0$. For all arriving aircraft $i,j \in A$ we have the separation constraint \begin{align} Z_{ij}^{*}(t_j - t_i - \delta_{ij}^{*}) \geq& 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \forall i,j \in A \end{align} which ensures that if arriving aircraft $j$ follows arriving aircraft $i$ at merge node P2 they should be separated by a minimum of $\delta_{ij}^*$, else the constraint is automatically satisfied. Given the sequencing constraint defined in (12), the value $\delta_{ij}^*$ should be non-negative else the constraint can not be satisfied.

For all departing aircraft $i \in D$ and arriving aircraft $j \in A$ we introduce the constraint \begin{align} a_{ij}^{LB} + a_{ij}^{UB} =& 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \forall i \in D, j \in A \end{align} where $a_{ij}^{LB}$ is a binary variable that is 1 for departing aircraft $i$ and arriving aircraft $j$ if we release the arriving aircraft $j$ into the center alley to the left of the lower bound of the conflict with departing aircraft $i$, see Figure, else $a_{ij}^{LB}=0$. Similarly $a_{ij}^{UB}$ is a binary variable that is 1 for departing aircraft $i$ and arriving aircraft $j$ if we release the arriving aircraft into the center alley to the right of the upper bound of the conflict with departing aircraft $i$.

For all departing aircraft $i\in D$ and arriving aircraft $j \in A$ we have the separation constraint \begin{align} a_{ij}^{LB} ( t_j - t_i - \Delta_{ij}^{LB}) \leq& 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \forall i \in D, j \in A \end{align} when $a_{ij}^{LB}=1$ this ensures the scheduled time $t_j$ that we release arriving aircraft $j$ into the ramp area is a minimum of $\Delta_{ij}^{LB}$ prior to the scheduled terminal time $t_i$ that we require departing aircraft $i$ to arrive at merge node P1.

For all departing aircraft $i \in D$ and arriving aircraft $j\in A$ we also have the separation constraint \begin{align} a_{ij}^{UB} ( t_j - t_i - \Delta_{ij}^{UB}) \geq& 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \forall i \in D, j \in A \end{align} when $a_{ij}^{UB}=1$ this ensures the scheduled time $t_j$ that we release arriving aircraft $j$ into the ramp area is a minimum of $\Delta_{ij}^{UB}$ after the scheduled terminal time $t_i$ that we require departing aircraft $i$ to arrive at merge node P1.

The output of the program is a schedule of merge node times $t_i$ that minimizes the summation of aircraft hold time. Furthermore, the model provides the feasible push back windows for each departing aircraft, as shown in Table 1. The right hand side of Table 1 shows the scheduled times and aircraft hold for a First-Come, First-Served (FCFS) scheduling approach. The FCSC scheduling approach is defined to schedule the aircraft at the taxiway spot in the same sequence that the aircraft become available to initiate their trajectories. The conservative conflict constraints are applied to the FCFS sequence of aircraft and the schedule is computed. As can be seen in the table, the FCFS scheduling approach is sub-optimal in comparison to the MILP approach.

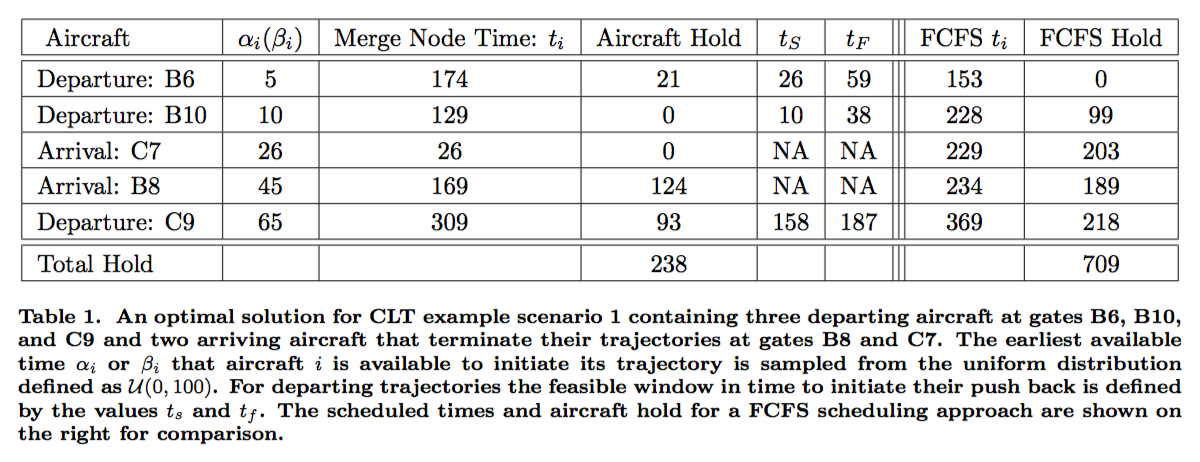
The example scenario that we consider in Table 1 is defined by three departing aircraft at gates B6, B10, and C9 and two arriving aircraft that terminate their trajectories at gates B8 and C7. For the given scenario, the optimal schedule and the associated aircraft hold times are dependent upon the set of sampled earliest available times $\alpha_i$ and $\beta_i$. For a different set of earliest available times $\alpha_i$ and $\beta_i$, the optimal schedule and aircraft hold times can be quite different. For a given scenario (set of departing and arriving aircraft), we would like to understand how our scheduling algorithm performs under a variety of different sets of earliest available times.

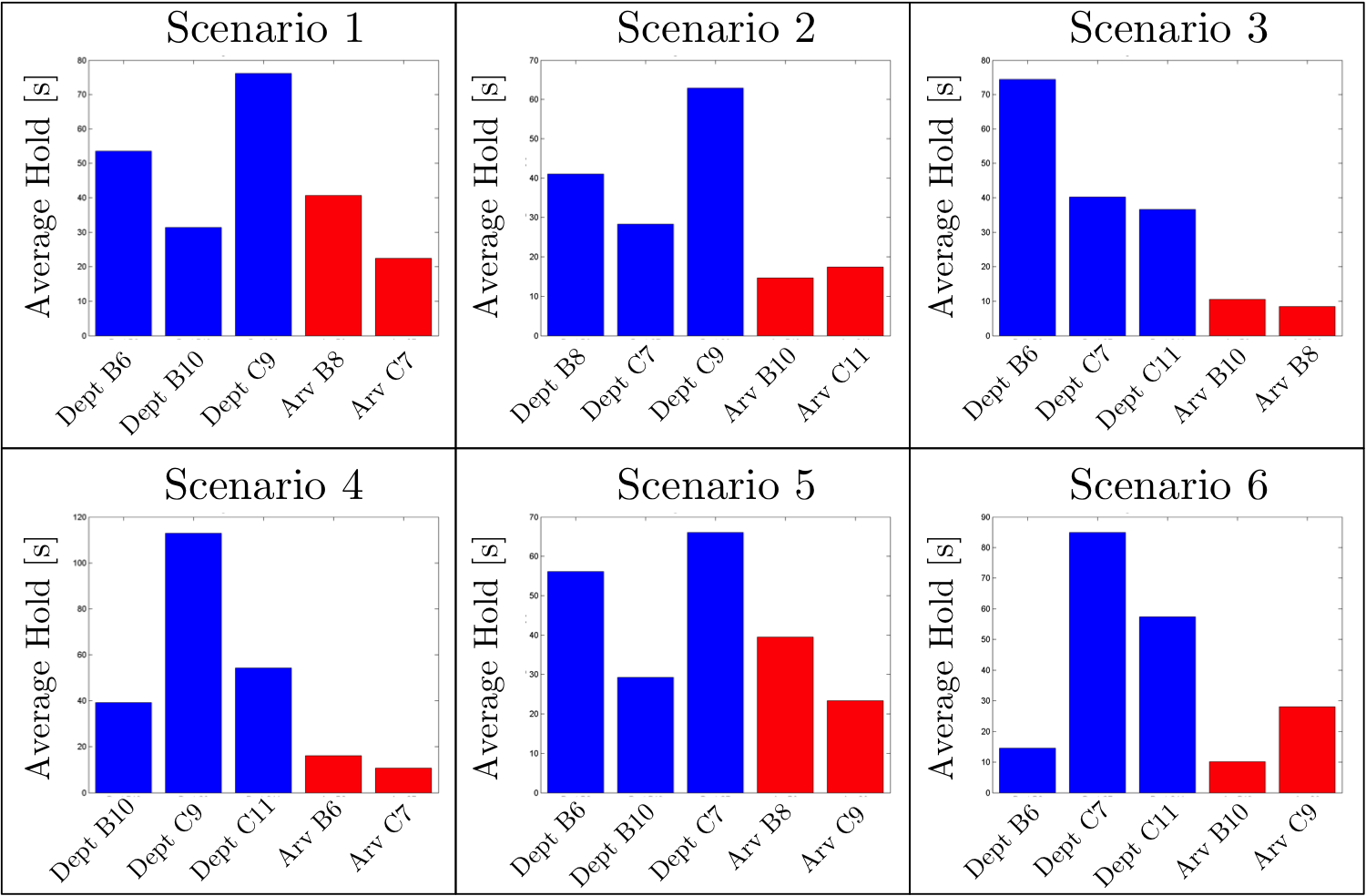
In order to understand the overall performance of the MILP we fix a scenario, compute the optimal schedule for many different sets of earliest available times, and then calculate the average hold times for each aircraft, as seen in each sub figure in the Figure below. Solutions for each scenario are computed for 300 randomly sampled sets of earliest available input parameters and the average hold time for each aircraft within the six different example scenarios is plotted. In the upper left most figure (scenario 1), the average hold time for departing aircraft from gates B6, B10 and C9 are shown with blue bars while the average hold time for arriving aircraft from gates B8 and C7 are shown with red bars. We apply the same analysis of averaging the hold time over many different sampled sets of earliest available times and apply it to five additional scenarios (sets of departing and arriving aircraft).