Code Snippets
Interesting code snippets for various uses
Breaking a Paragraph into Lines
Category: Dynamic Programming
Given a sequence of words \( w_{1} \dots w_{n} \) we need to insert them into a paragraph where we penalize the empty space at the end of each line. Let the width of each line be \(W\) and the space required to fit words \(w_{i} \dots w_{j}\) be \(y(i,j)\) then the total penalty we incur is \( \sum_{i=0}^{m} P(W, y(i,j)) \) where \(P\) is a generic increasing loss function and \(m\) is the number of lines we output. The lines of the paragraph are defined by a sequence of breakpoints \( \{b_{1}, \dots b_{m}\} \), where, \( b_{i} \) means that we start a new line starting with word \( i \). Finally, the goal is to output the optimal sequence of breakpoints \( b_{1} \dots b_{m} \) so as to minimize the cost function \( P \). In this problem we make the assumption that the first line does not incur any penalty.
We approach this problem using Dynamic Programming. Consider the optimal solution \( \mathcal{O} \) to to this problem, then given we are considering the \( i^{th} \) word we have to decide on which line to insert it. We can create a new line and insert words \( w_{j}, w_{j+1} \dots w_{i} \) for some index \( j \) such that \(y(j,i) \leq W \), in order for the sequence of words to fit in the same line. Let \( q(i)\) be a function that outputs the least \(j\) such that we can fit \(w_{j} \dots w_{i}\) on the same line. Then we have to find the optimal breakpoint \(b_{j}\) and then behave optimally for the sequence \(w_{1} \dots w_{j-1}\). These observations suggest that we should look into subproblems that include the first \(i\) words of the sequence.
Hence, let \( OPT(i) \) be the optimal cost of breaking the sequence of the first \( i \) words into a paragraph. Then if \( i = 0 \) then the cost of breaking no words is also \( 0 \). In general for \( i > 0 \) we get: $$ OPT(i) = \min\limits_{q(i) \leq k \leq i} \{ OPT(k-1) + P(W, y(k,j) \} $$ Our goal is to compute \( OPT(n) \). To do this, based on the above identity we form a \( 1D \) array, say \( M \), to store the optimal value. We proceed to fill out \( M \) in the following order. First we fill in \(M[0]=0\). In general we notice that in order to fill entry \(i\), of \(OPT\), we need to know the value at entries \(q(i),q(i)+1, \dots i-1\). Therefore we can fill \(M\) by increasing \(i\) and compute the cases where \(y(0,n) \leq W\) directly from the above recurrence. In order to calculate a particular entry for the array \(M\), takes \(O(n)\) time since we take a minimum of (at most) \(n\) numbers . Since there is a total of $n$ entries, we get that the running time of this algorithm is \(O(n^{2}) \).
My code for the problem
import numpy as np
def space(index_i, index_j, maxWidth, par):
''' returns the space (characters) needed for words
indexed from i to j to be stored including
spaces betweem different words '''
c = 0
for i in range(index_i, index_j+1):
c += len(par[i])
c += index_j - index_i #gaps between words
return c
def init(maxWidth, par):
'''
Let s(i,j) be the space left if we put words
starting at i and ending at j in the same sentence
Let q(i) be the min indexed word that we could break up
the sentence if we consider a line ending at i
'''
s = np.zeros((len(par), len(par)), dtype = int)
q = np.zeros(len(par), dtype = int)
#initialize s
for i in range(len(par)):
for j in range(len(par)):
if j >= i:
s[i,j] = space(i, j, maxWidth, par)
#initialize q
for j in range(len(par)):
temp = np.Inf
for i in range(j+1):
if temp > i and s[i,j] <= maxWidth:
temp = i
q[j] = temp
return s, q
def cost_third_function(margin):
''' Cost function to penalize "slack" '''
return margin**3
def cost_square_function(margin):
''' Cost function to penalize "slack" '''
return margin**2
def break_par(maxWidth, sentence, penalize_First = False, cost_function = cost_square_function):
'''
outputs a set of breakpoints as well as
the corresponsing optimal score. In this implementation
the first line has no penalty whereas all the other lines have
penalties. The convention is that if the breakpoint is b_i,
then this means that a new line starts at the beginning of word i.
By default we do not penalize the first line and use the square function
to penalize the margin. You can define your costum cost_function and pass it
as a parameter to this function.
'''
par = [i for i in sentence.split()]
#guard against invalid input
for i in par:
if len(i) > maxWidth:
print("Lenght of each word must be less than W. Aborting.")
return
s, q = init(maxWidth, par)
#this takes care of opt[0] = 0
opt = np.zeros(len(par))
b = np.zeros(len(par), dtype = int) #hold breakpoints
for i in range(1, len(par)):
temp_min = np.Inf
for k in range(q[i], i+1):
if penalize_First == False: # if do not penalize the first line
if k == 0 and temp_min > opt[k-1]:
temp_min = opt[k-1] #no penatly in the first line
b[i] = k
elif temp_min > opt[k-1] + cost_function(maxWidth - s[k,i]) :
temp_min = opt[k-1] + cost_function(maxWidth - s[k,i])
b[i] = k
else: # if we want to penalize the first line
if temp_min > opt[k-1] + cost_function(maxWidth - s[k,i]) :
temp_min = opt[k-1] + cost_function(maxWidth - s[k,i])
b[i] = k
opt[i] = temp_min
#subtle point in the code
#we basically do not want all the
#breakpoints in b since we "overwrite" all
#the breakpoints from q[i] to i every time we
#consider the ith word
last_k = b[-1]
good_breaks = []
while last_k >= 1:
good_breaks.append(last_k)
last_k = b[last_k-1]
good_breaks.append(0)
good_breaks.reverse()
return good_breaks, opt[-1]
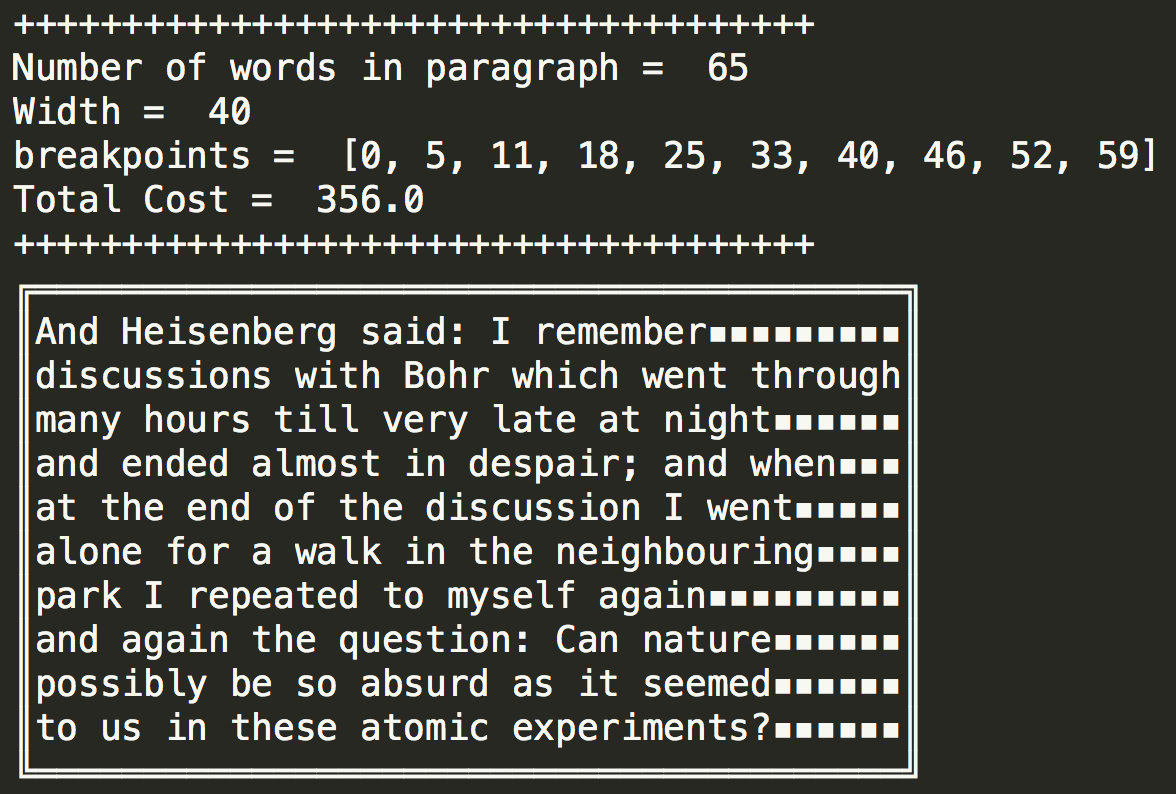
def print_par(maxWidth, sentence, breakpoints, cost = None):
''' Pretty printing of paragraph given breakpoints '''
par = [i for i in sentence.split()]
print "+++++++++++++++++++++++++++++++++++++"
print "Number of words in paragraph = ", len(par)
print "Width = ", maxWidth
print "breakpoints = ", breakpoints
if cost is not None:
print "Total Cost = ", cost
print "+++++++++++++++++++++++++++++++++++++"
#create upper side of the box
print u'\u2554' + u'\u2550'* (maxWidth) + u'\u2557'
for i in range(len(breakpoints)):
if i == len(breakpoints) - 1: #case of last index dump everything
s = ' '.join(par[breakpoints[i]:])
print u'\u2551'+ s + u'\u25AA' * (maxWidth-len(s)) + u'\u2551'
else:
s = ' '.join(par[ breakpoints[i] : breakpoints[i+1]])
print u'\u2551'+ s + u'\u25AA' * (maxWidth-len(s)) + u'\u2551'
#create lower side of the box
print u'\u255A'+ u'\u2550' * (maxWidth) + u'\u255D'
print '\n'
def main():
W = 8
s2 = 'aa bbbbb c'
#breakpoints2, cost2 = break_par(W, s2, cost_function = cost_third_function)
#print_par(W, s2, breakpoints2, cost2)
s3 = 'aa bbbbb c d'
#breakpoints3, cost3 = break_par(W, s3, cost_function = cost_third_function)
#print_par(W, s3, breakpoints3, cost3)
W = 12
s1 = ' "Do only what only you can do" '
#breakpoints1,cost1 = break_par(W, s1, cost_function = cost_third_function, penalize_First = True)
#print_par(W, s1, breakpoints1, cost1)
W = 40
s0 = '''And Heisenberg said: I remember discussions with
Bohr which went through many hours till
very late at night and ended almost in despair;
and when at the end of the discussion I went alone
for a walk in the neighbouring park I repeated to
myself again and again the question:
Can nature possibly be so absurd as it seemed to
us in these atomic experiments?'''
#breakpoints1,cost1 = break_par(W, s0, penalize_First = True)
#print_par(W, s0, breakpoints1, cost1)
Example Usage with the Cubic loss function
And Heisenberg said: I remember discussions with Bohr which went through many hours till very late at night and ended almost in despair; and when at the end of the discussion I went alone for a walk in the neighbouring park I repeated to myself again and again the question: Can nature possibly be so absurd as it seemed to us in these atomic experiments?
Now by defining the line width to be 40 characters and then running this script on the input displayed above we get: