Hiroyuki Takeda, Prof. Peyman Milanfar$
Abstract
The need for precise (subpixel accuracy) motion estimates in conventional super-resolution has limited its applicability to only video sequences with relatively simple motions such as global translational or affine displacements. In this work, we introduce a novel framework for adaptive enhancement and spatiotemporal upscaling of videos containing complex transitions without explicit need for subpixel motion estimation.
Using some examples shown below, we illustrate that our algorithm has resolution enhancement capabilities that provide improved optical resolution in the output, while being able to work on general input video with essentially arbitrary motions.
Related
publications:
H.
Takeda and P. Milanfar,"Locally
Adaptive Kernel Regression for Space-Time Super-Resolution",
To appear as a Chapter in Super-resolution
Imaging Edited by P. Milanfar, Available September 27,
2010.
Takeda, H., P. Milanfar, M. Protter, and M. Elad, "Superresolution
without Explicit Subpixel Motion Estimation", IEEE
Transactions on Image Processing, Vol. 18, No. 9, September 2009.
Takeda, H., S. Farsiu, and P. Milanfar, "Kernel Regression for Image Processing and Reconstruction", IEEE Transactions on Image Processing, Vol. 16, No. 2, pp. 349-366, February 2007.
Space-Time Video Upscaling
3-D Steering Kernel Regression
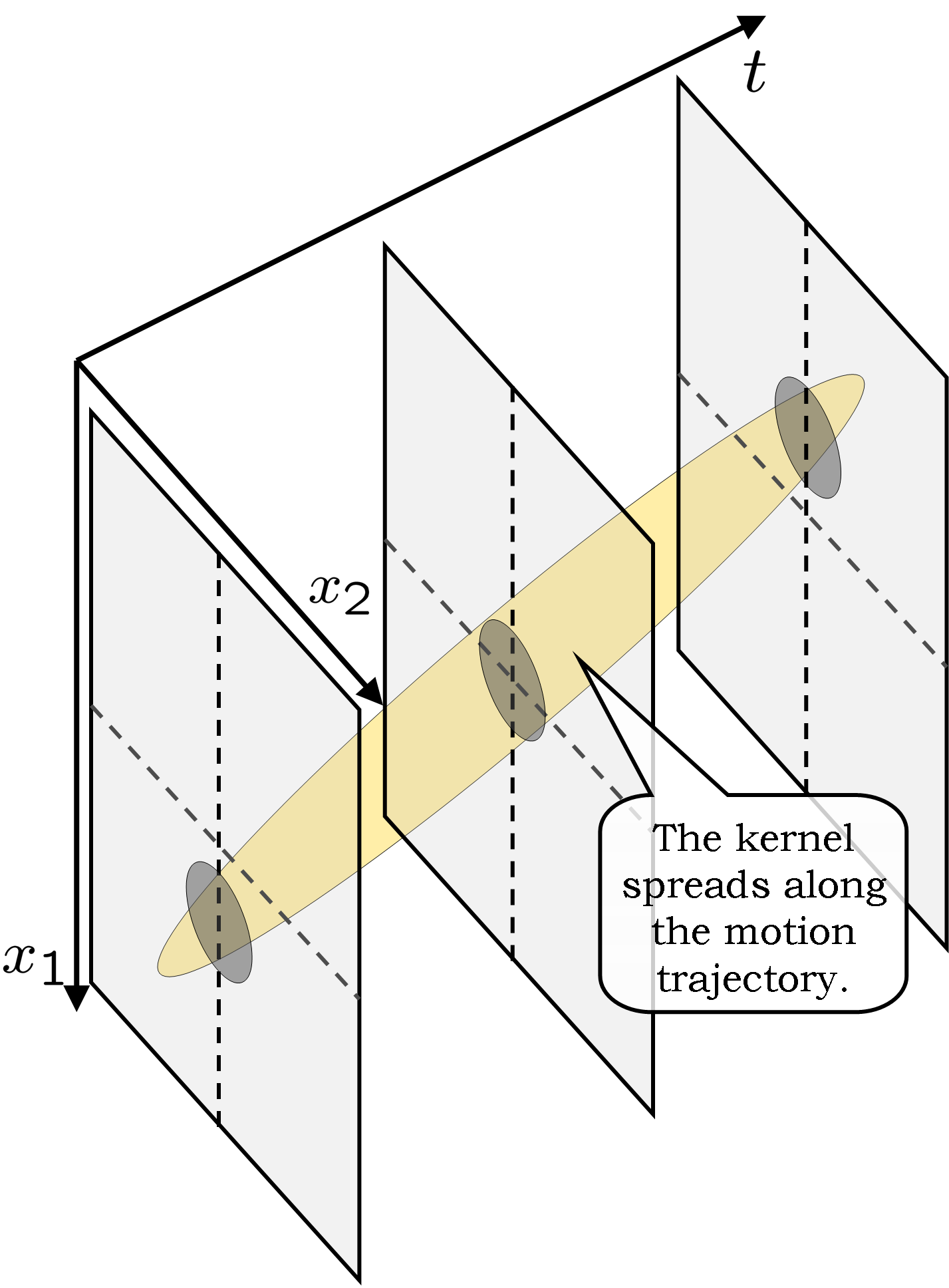
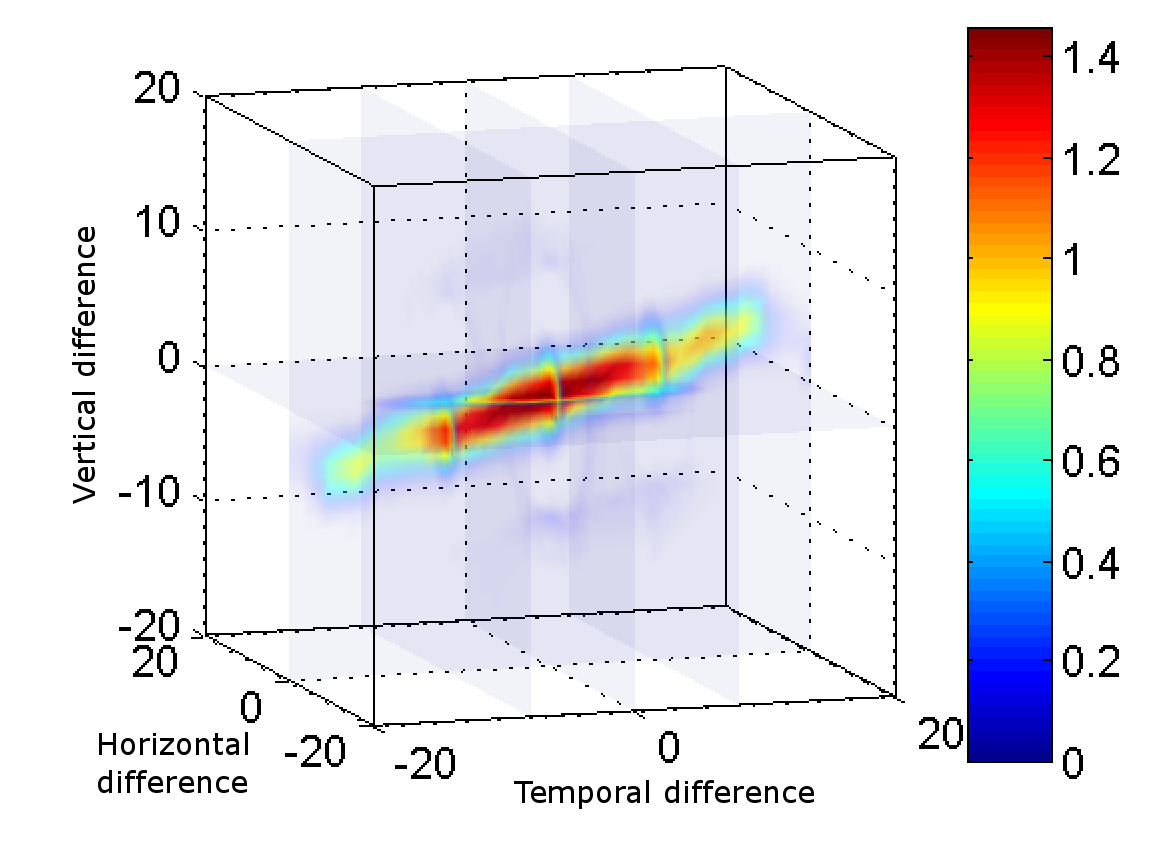
Our approach is based on multi-dimensional (3-D) kernel regression, where each pixel in the video is approximated with a 3-D local polynomial (Taylor) series, captureing the essential local behavior of its spatiotemporal neighborhood. The coefficients of this series are estimated by solving a local weighted least-squares problem, where the weights are a function of the 3-D space-time orientation in the local analysis cubicle. As this method is fundamentally based upon the comparison of neighboring pixels in both space and time, it implicitly contains information about not only the spatial orientation structures but also the local motion trajectories across time (see Figure 1 below). Therefore rendering unnecessary an explicit computation of motions of modes size
 (a) A local region |
 (b) Steering kernel weights |
Implementation
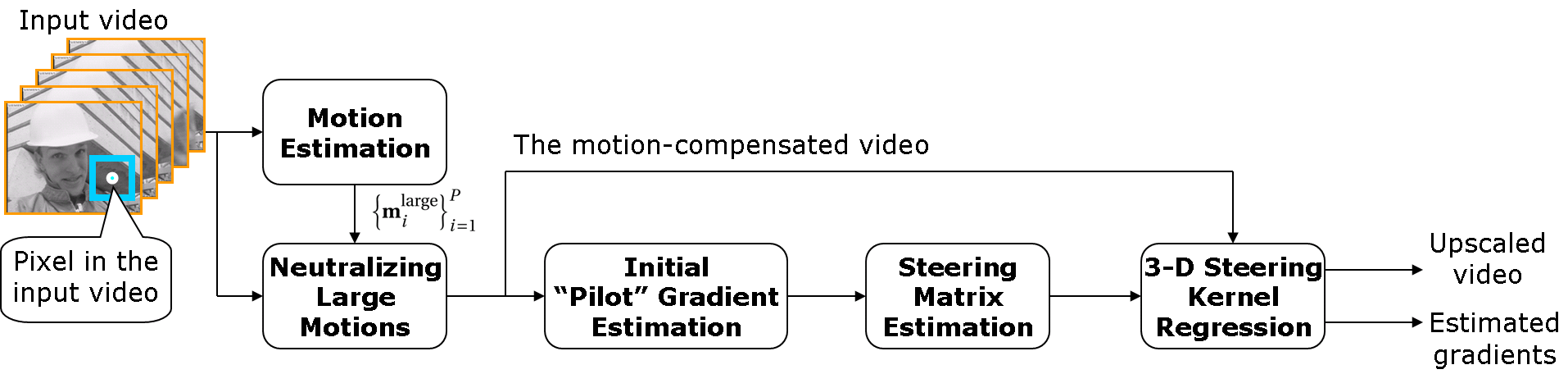
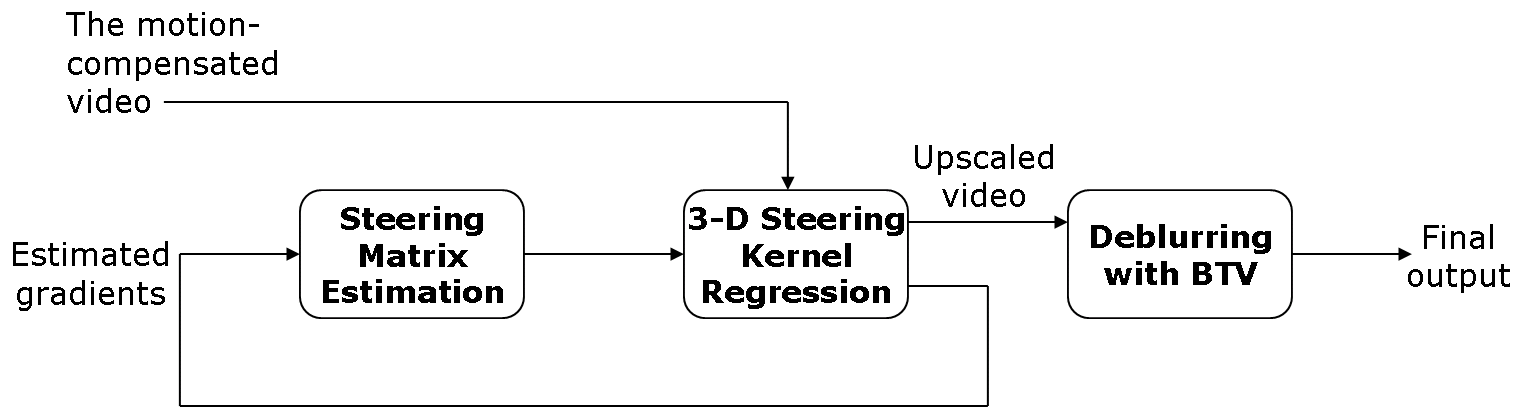
When the speed of the local motions is relatively large, a mechanism for neutralizing such displacements roughly (to within a whole pixel accuracy) is introduced, which may be called coarse motion compensation. Within this framework, the remaning fine scale (subpixel) motions are then captured using the 3-D kernel regression. Figure 2 shows the block diagram of the 3-D SKR method with motion compensation and an iteartive scheme. The proposed approach not only significantly widens the applicability of super-resolution methods to a variety of video sequences contaning complex motions, but also yields improved overall perfomance.
 (a) Initialization |
 (b) Iteration |
Examples
 
|
||||

The output video is also available here. The video shows the input frames in the left, the upscaled frames by Lanczos, NLM-based SR, and 3-D SKR in the second left, the second right, and the right, respectively. |
2. Spatiotemporal upscaling example

|
|||||||||||||||||||||||
A video upscaling example of Stefan sequence
The results are also available in video (AVI) format here. The video shows the original frames ( left), the upscaled frames by 3-D linear interpolation (middle), and the upscaled frames by 3-D SKR with motion compensation (right). For this video, we used the spatial upscaling factor 1 : 2 and temporal upscaling factor 1 : 10, and deblurred all the frames one-by-one with the 2x2 uniform PSF and BTV regularization. |
Software
The software package of the space-time steering kernel regression for MATLAB is downloadable from here. The user's manual is also available as either PPT or PDF.
This is a package of the experimental codes. It is provided for noncommercial research purposes only. Use at your own risk. No warranty is implied by this distribution. Copyright © 2010 by University of California, Santa Cruz.











