Thesis Research
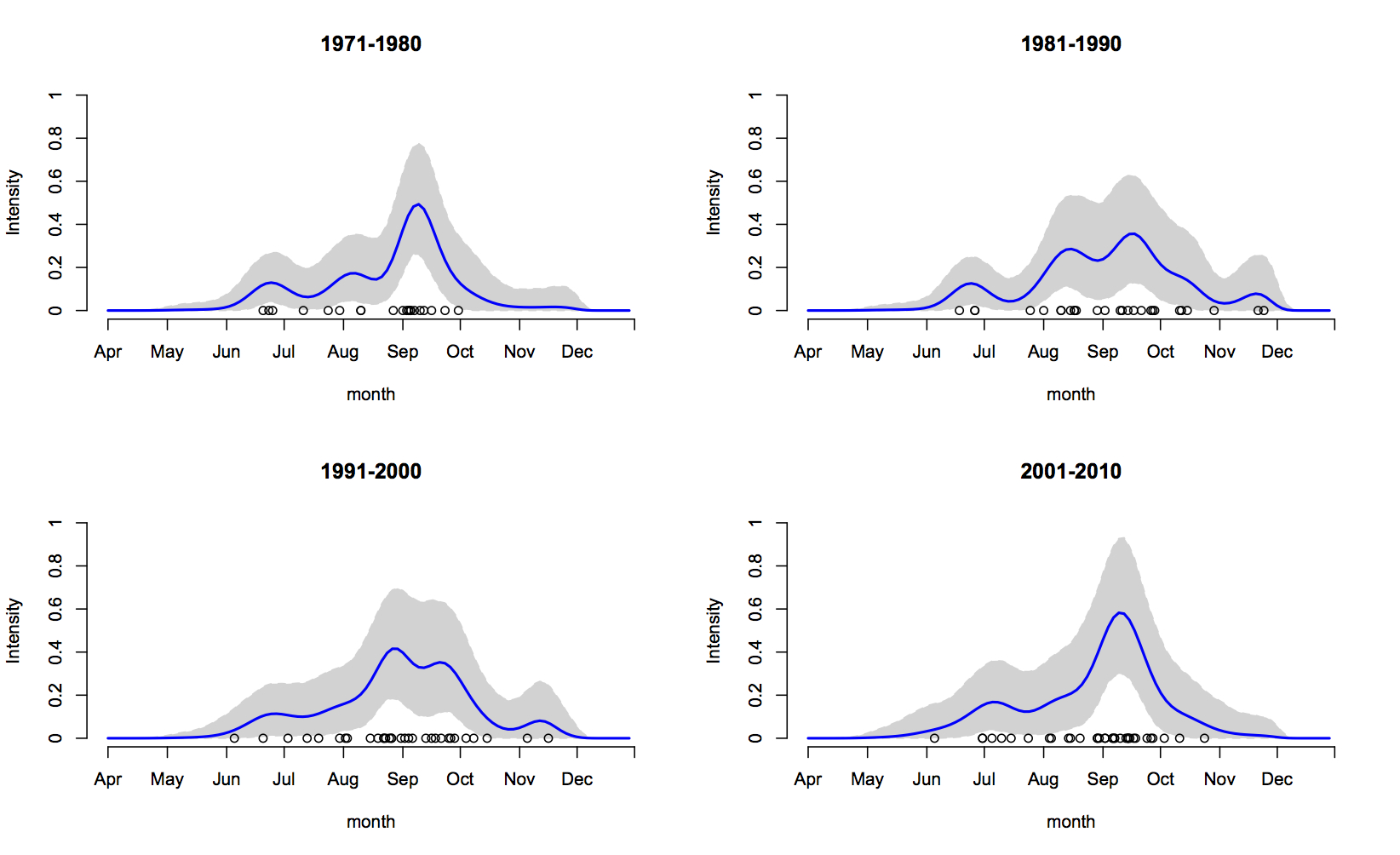
 We explore a Bayesian non-parametric method to model the time varying intensity of seasonal point processes along with the associated marks. The basic assumption is the points follow a non-homogeneous Poisson process (NHPP). We decompose intensity function as normalizing constant and density function to solve the intractability issue of likelihood of NHPP. The main techniques in the model in- clude using the dependent Dirichlet mixture models and time series models. Variance inferences and forecast can be obtained to reveal the characteristics of time-dependent intensity function and conditional density of marks. The work focus on application in hurricane landfalls along US Gulf and Atlantic coast over 100 years.
We explore a Bayesian non-parametric method to model the time varying intensity of seasonal point processes along with the associated marks. The basic assumption is the points follow a non-homogeneous Poisson process (NHPP). We decompose intensity function as normalizing constant and density function to solve the intractability issue of likelihood of NHPP. The main techniques in the model in- clude using the dependent Dirichlet mixture models and time series models. Variance inferences and forecast can be obtained to reveal the characteristics of time-dependent intensity function and conditional density of marks. The work focus on application in hurricane landfalls along US Gulf and Atlantic coast over 100 years.
This work won the SBSS student travel award 2014.
The code and documentation can be downloaded from here.
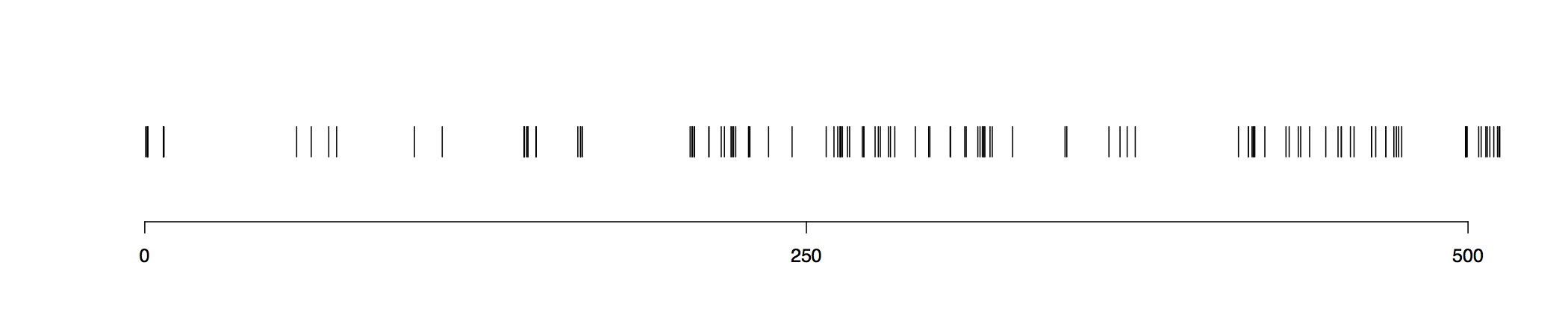
We build models to accommodate departures from the Poisson process assumption to tackle more realistically some of the applications considered in this research. We begin to focus on Bayesian non-parametric modeling for homogeneous renewal process. The model provides flexible shapes of inter-arrival time densities and is capable of modeling point processes with clustering or regularity pattern.
An extension of homogeneous renewal point process to Markov renewal process. This model will introduce time-dependency into the intensity function.
Course project