Any image can be represented as a function defined on a weighted graph, in which the underlying structure of the image is encoded in kernel similarity and associated Laplacian matrices. In this paper, we develop an iterative graph-based framework for image restoration based on a new definition of the normalized graph Laplacian. We propose a cost function which consists of a new data fidelity term and a regularization term derived from the specific definition of the normalized graph Laplacian. The normalizing coefficients used in the definition of the Laplacian and the associated regularization term are obtained using fast symmetry preserving matrix balancing. 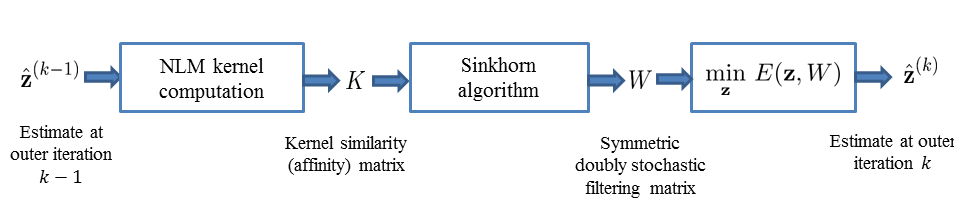This results in some desired spectral properties for the normalized Laplacian such as being symmetric, positive semi-definite, and returning zero vector when applied to a constant image. Our algorithm comprises of outer and inner iterations, where in each outer iteration, the similarity weights are recomputed using the previous estimate and the updated objective function is minimized using inner Conjugate Gradient (CG) iterations. This procedure improves the performance of the algorithm for image deblurring, where we do not have access to a good initial estimate of the underlying image. Moreover, the specific form of the cost function allows us to render the spectral analysis for the solutions of the corresponding linear equations. Also, the proposed approach is general in the sense that we have shown its effectiveness for different restoration problems including deblurring, denoising, and sharpening. Experimental results verify the effectiveness of the proposed algorithm on both synthetic and real examples.

Overview of the proposed method

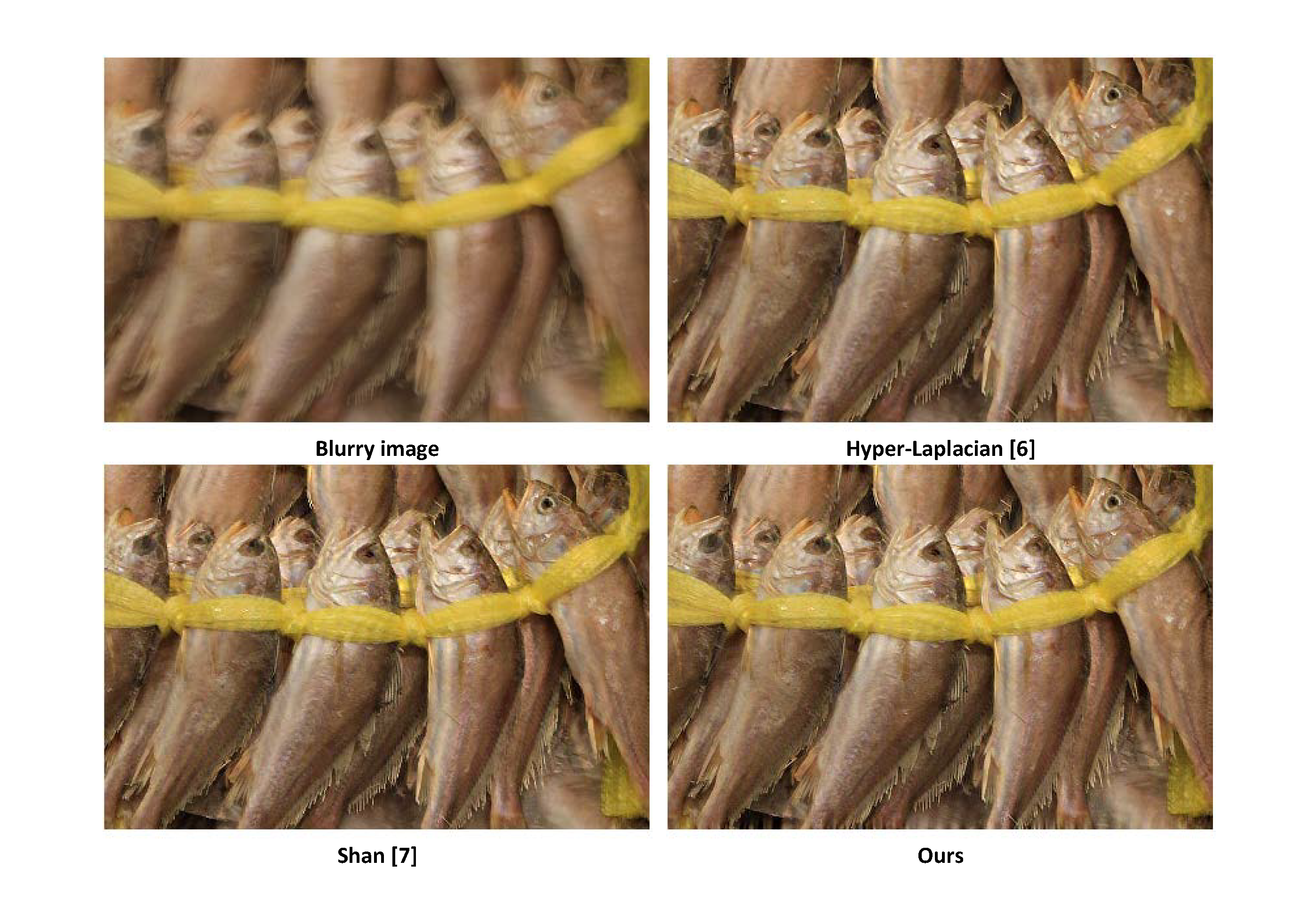
Deblurring examples

Sharpening examples

MATLAB Code

References